Vennovy diagramy
 V matematice se snažíme používat jednoduché a názorné pomůcky pro vizuální představu množin, vztahů mezi nimi a operacemi s nimi. Vhodným nástrojem při zavádění a procvičování průniku, sjednocení, rozdílu množin a doplňku množiny v množině jsou Vennovy diagramy. Správné používání Vennových diagramů vyžaduje dobrou orientaci v těchto diagramech a pochopení vztahů mezi jednotlivými částmi konkrétního diagramu. Pomocí Vennových diagramů také můžeme řešit nejrůznější logické úlohy, které nám život přináší. Jejich další využití je při řešení slovních úloh, ve kterých se určují počty prvků konečných množin.
V matematice se snažíme používat jednoduché a názorné pomůcky pro vizuální představu množin, vztahů mezi nimi a operacemi s nimi. Vhodným nástrojem při zavádění a procvičování průniku, sjednocení, rozdílu množin a doplňku množiny v množině jsou Vennovy diagramy. Správné používání Vennových diagramů vyžaduje dobrou orientaci v těchto diagramech a pochopení vztahů mezi jednotlivými částmi konkrétního diagramu. Pomocí Vennových diagramů také můžeme řešit nejrůznější logické úlohy, které nám život přináší. Jejich další využití je při řešení slovních úloh, ve kterých se určují počty prvků konečných množin.
Tento způsob znázornění množin navrhl v roce 1881 anglický matematik a filosof John Venn (1834 – 1923) ve své knize Symbolická logika. Vennův diagram tvoří uzavřená křivka, přičemž body uvnitř křivky představují prvky množiny a body vně křivky představují body, které do množiny nepatří. Obvykle předpokládáme, že na křivce neleží žádné body. Vennův diagram je jedna z možností zadání prvků množiny. Množinové úvahy se obvykle týkají malého počtu množin. Situace zahrnující dvě, tři nebo čtyři množiny přehledně znázorňujeme systémem přihrádek - Vennovy diagamy pro 2, 3, 4 množiny. Tato schémata vznikají překřížením uzavřených čar. Při znázornění dvou
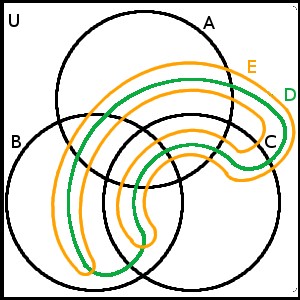 n křivek vytváří 2 na entou polí v rovině nebo ve vnitřní oblasti předem zvolené křivky. Na obrázcích vidíme Vennovy diagramy pro 4 množiny a pro 5 množin (ta pátá je ohraničena oranžovou křivkou)
n křivek vytváří 2 na entou polí v rovině nebo ve vnitřní oblasti předem zvolené křivky. Na obrázcích vidíme Vennovy diagramy pro 4 množiny a pro 5 množin (ta pátá je ohraničena oranžovou křivkou)
Tam, kde je znázornění množin pomocí Vennových diagramu nevhodné, používáme jejich znázornění na číselné ose.
Pro lepší orientaci v problému přikládám odkaz: https://astra.karlin.mff.cuni.cz/katedry/kdm/diplomky/moravecdp/mnoziny.php