Collatzův problém
 Collatzův problém je jedním z dosud nevyřešených matematických problémů. Je pojmenován po Lotharu Collatzovi, který jej poprvé formuloval v roce 1937. Tento problém je znám pod různými názvy: jako 3n + 1 problém, Ulamův problém (po Stanislawu Ulamovi), Syrakuský problém či sekvence ledové kroupy.
Collatzův problém je jedním z dosud nevyřešených matematických problémů. Je pojmenován po Lotharu Collatzovi, který jej poprvé formuloval v roce 1937. Tento problém je znám pod různými názvy: jako 3n + 1 problém, Ulamův problém (po Stanislawu Ulamovi), Syrakuský problém či sekvence ledové kroupy.
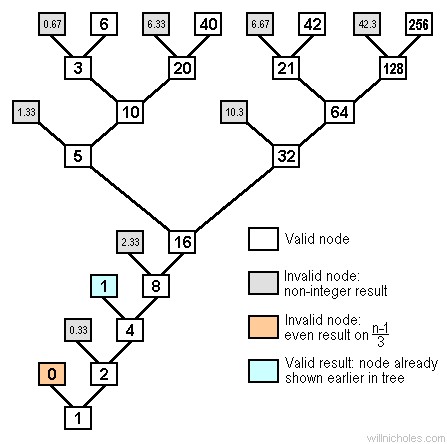
V tomto problému se jedná o rozklad čísel. Čím je číslo větší, tím je jeho rozklad složitější. Metoda spočívá v tom, že pokud je číslo sudé, tak jej vydělíme dvojkou (n/2), pokud je liché, tak jej vynásobíme třemi a přičteme jedničku (3n + 1). Takto postupujeme až se nakonec dostaneme k číslu jedna.
Například: máme číslo 20
20/2 = 10/2 = 5*3+1 = 16/2 = 8/2 = 4/2 = 2/2 = 1
Hypotéza tvrdí, že každé číslo by mělo jít touto metodou rozložit, záleží pouze na počtu operací. Ke každému číslu se matematikové snaží najít počet operací a zároveň potvrdit že jde takto rozebrat opravdu každé číslo. Collatzův problém říká, že tento proces se vždy zastaví, bez ohledu na to, jaké číslo bylo na samém začátku.
Na internetu se také můžete zúčastnit práce na projektu s názvem: 3x+1@home. Projekt se zabývá zpracováním čísel větších než 21 000. Výsledky se pak používají například pro generování fraktálů.
Důkaz Collatzova problému nebyl ještě publikován. Matematik Paul Erdös řekl o Collatzovu problému: "Matematika není ještě připravena na tyto problémy." A věnoval 500 dolarů na jeho řešení.
V roce 2006 výzkumníci Kurtz a Simon v návaznosti na dřívější práce Conwaye v 1970 napsali, že fyzická generalizace z Collatzova problému je rekurzivně nerozhodnutelná.
Pokud je z problému odstraněna podmínka ukončení ("jestliže n = 1”) pak sekvence neskončí. Sekvence potom vždy skončí ve smyčce opakování: 1, 4, 2, 1, 4, 2...
Až se budete někdy nudit, tak můžete hledat nejdelší posloupnost začínající číslem menším než jeden milion. Který začínající prvek menší než jeden milion vytvoří nejdelší posloupnost? Ačkoli první prvek posloupnosti je menší než 1 milion, ostatní prvky mohou být i větší.
Komentáře
| RE: Collatzův problém | výborně! | 02. 06. 2010 - 19:29 |
| fyzmatik | 03. 06. 2010 - 17:39 | |
| wrunx | 21. 08. 2012 - 20:54 | |
| fyzmatik | 22. 08. 2012 - 09:02 | |
| wrunx | 14. 09. 2012 - 22:53 | |
| jklmn203 | 30. 09. 2016 - 21:47 | |
| RE: Collatzův problém | ye | 24. 09. 2010 - 11:18 |