Zkoušeli jste si někdy vzít pořádné noviny a postupně je skládat na poloviny? Zprvu to vypadá, že se nám podaří noviny složit minimálně desetkrát, ale postupně nám vzniká malý tuhý a neforemný balíček papíru, který brání dalšímu přeložení. Kolikrát jste přeložili list papíru?

Kravata patří více než 350 let k reprezentativnímu oblečení každého seriózního muže. Plní jednak funkci estetickou - to pro ty ostatní, pro nositele kravaty to často bývá oblíbený mučící nástroj. Navíc s ďábelským úkolem, jak ji správně uvázat. Matematika zkoumá i způsoby vázání kravat.

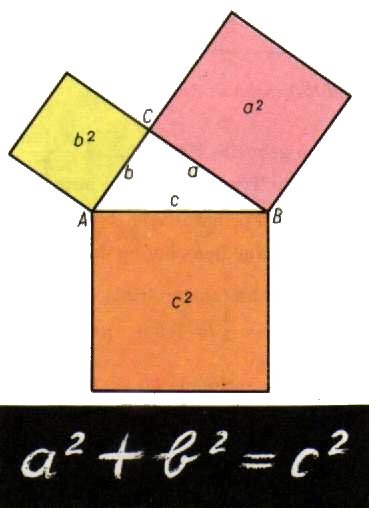Kdo by neznal snad nejslavnější matematickou větu - Pythagorovu.
Pythagorova věta zní: "Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníka je roven součtu obsahů sestrojených čtverců nad jeho odvěsnami".

Přeponou nazýváme nejdelší stranu trojúhelníku, která leží proti pravému úhlu, odvěsnami pak kratší strany ležící proti zbývajícím úhlům.

Věta byla nazvána podle Pythagora, který ji někdy v 6. století př. n. l. znovuobjevil pro starověké Řecko.

Tato věta však byla známa i v jiných starověkých civilizacích dávno předtím (v Číně, částečně např. v Egyptě).

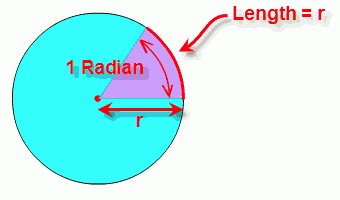Rovinný úhel může být definován jako část roviny určená dvěma polopřímkami ležícími v této rovině se společným počátkem. Měření velikosti úhlů nemá v běžném životě takový význam jako například měření délky či hmotnosti. Zprvu bylo důležité zejména pro zeměměřiče, architekty, námořníky a hlavně astronomy. Obvykle se úhly měřily ve stupních a minutách, ke kterým se pro zpřesnění přidaly později úhlové vteřiny. Jak se však k těmto jednotkám přišlo?

Paul Adrien Maurice Dirac ( 1902 –1984) byl anglický teoretický fyzik, který se zabýval kvantovou teorií, obecnou teorií relativity a kosmologií. Za svoji základní práci v kvantové fyzice získal v roce 1933 společně s Erwinem Schrödingerem Nobelovu cenu. Dirac měl schopnost předvídat neočekávané jevy a hledat netradiční řešení problémových úloh. Předpověcděl existenci antičástic. Už jako student údajně předložil v matematické soutěži vlastní netradiční řešení jedné úlohy.

Odvěkou snahou matematiků je co nejpřesnější vyjádření Ludolfova čísla. Ludolfovo číslo je označení čísla π. Jméno získalo podle Holanďana Ludolpha von Ceulen, který už v roce 1596 vypočítal číslo π nejprve na 20 desetinných míst a později v roce 1615 je zpřesnil na 35 desetinných míst. Číslo pí bylo známo dávno. V období antiky (kolem 2000 př. n. l.)  používali Babyloňané k výpočtu zlomek 25/8 = 3,125. V Egyptě byla používaným vztahem hodnota zlomku 22/7 = 3,14285. Přesnou aproximaci čísla pí provedl Archimédés. Pomocí vepsaných a opsaných mnohoúhelníků ke zvolenému kruhu určil, že se nachází v intervalu od 3 +10/71 až 3 + 10/70. Jak jej vyjádřit co nejjednodušeji a přitom s přesností na více desetinných míst?

Každým dnem se přesvědčujeme, že lidé věří na magii a podobné nesmysly. Ani znalost násobilky a odečítání u mnohých jedinců nestačí na pochopení jednotlivých kouzelnických triků. A tak nás v televizi David Copperfield může udivovat zázraky typu: mysli si číslo a pak dej prst na obrazovku a zobrazí se ti správné číslo či symbol na který jsi myslel. Na obrazovce nám kouzelník poskytne pouze jednu možnost na odhalení triku, proto většina diváků princip kouzla neodhalí a považují jej div ne za zázrak. Přitom nám na odhalení některých triků stačí znalost malé násobilky a úpravy výrazů. Co takhle vypořádat se s magickou koulí, která odhalí symbol na který myslíte?

Ze všech čísel jsou mezi matematiky oblíbena zvláště prvočísla. Těch je několik druhů. Dnes se zaměříme na tzv. palindromická prvočísla. Palindrom je slovo řeckého původu, které znamená" běžet znovu zpátky". Palindromem pak rozumíme sekvenci znaků - slovo, věta, číslo či dokonce prvočíslo, která se čte (odhlédneme-li od diakritiky a mezer) stejně zleva doprava či nazpátek a přitom má stejný význam. Mým oblíbeným matematickým palindromem je: "V elipse spí lev".

Velmi pěknou aplikací prvočísel v praxi jsou kódy knížek. Jsou označovány jako ISBN kódy a stejně jako rodná čísla jsou chráněny proti možné chybě samoopravným mechanismem. Tento systém mezinárodního standardního číslování knih - ISBN (International Standard Book Numbering) vznikl v Anglii na návrh profesora Gordona Fostera. Sdružení britských vydavatelů jej pověřilo návrhem jednoznačného číslování vydávaných knih. Foster v roce 1966 navrhl systém používající devíticiferné kódy. Ten byl zpočátku používán v Anglii a Postupně se rozšířil do více než 180 zemí. V České republice je zaveden od roku 1989. V tomto roce poprvé u nás vyšla také má nejoblíbenější kniha pod kódem ISBN 80-204-0023-0.

Pro přesná měření délek předmětů především ve strojírenství se používá posuvné měřítko - takzvaná šupléra (z německého Schub-lehre). Na ní si můžeme ukázat zajímavé praktické použití nesoudělných čísel. Měřítko se skládá ze dvou částí. Na pevné části je základní stupnice v níž je každý centimetr rozdělen na 10 mm. K pevné části pevně přiléhá posuvná část zvaná nonius, rozdělený na 10 stejně velkých dílků, které však dohromady měří jen 9 mm.