V technické praxi se setkáváme s potřebou zobrazování prostorových útvarů. I když dnes existují počítačové programy, které to pohodlně umožňují, je nutné se seznámit s pravidly zobrazování. Věda, která se zabývá zobrazováním prostorových útvarů do roviny (průmětny) se nazývá deskriptivní geometrie. Její počátky souvisejí se znázorňováním staveb na nákresy a plány.  Už před 4300 lety používali Chaldejci pravoúhlé promítání na jednu průmětnu při stavbách silnic, akvaduktů, chrámů apod. i pyramid. zobrazovací metody byly zdokonalovány nejenom pro potřeby stavitelství, ale také pro potřeby malířství. Od 15. století se začala používat  lineární perspektiva a po ní  dochází k rozvoji rovnoběžného promítání, a to nejdříve kosoúhlého. To bylo využíváno především ve vojenství, a to hlavně k zobrazování celých měst nebo jejich významných částí.

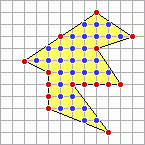Výpočet obsahu plochy ohraničeného mnohostranným (polygonálním) útvarem, který vznikne pospojováním bodů v mřížových bodech lze provést pomocí Pickova vzorce. Georg Pick byl rakouský matematik, který přijal v roce 1880 na Karlo-Ferdinandově univerzitě v Praze místo pomocného asistenta  významného fyzika Ernsta Macha. Pick byl blízkým přítelem Alberta Einsteina a v roce 1911 jej pozval, aby  působil na německé části Karlovy univerzity v Praze. Pick se zabýval především geometrií a proslavil se v geometrii mřížových bodů vzorcem, který po něm dostal jméno.

Mezi málo známá tělesa patří kaleidocykly. Jedná se o mnohostěnnou plochu tvořenou prstencem z pravidelných čtyřstěnů, které jsou navzájem propojeny svými hranami. S těmito zajímavými tělesy přišel před více než 100 lety německý učitel matematiky Max Brückner. Jeho nápad se zalíbil kanadskému geometru Coxeterovi (1907 - 2003), který šest shodných pravidelných čtyřstěnů (tetraedrů) spojil do prstýnku a zjistil, že při osmi a více takto spojených tetraedrech je možné prstýnek neustále protáčet středem. Liché počty tetraedrů lze také spojovat a protáčet. Při 22 spojených tetraedrech je možné z takto dlouhého prstýnku vytvořit propletený uzel.

Krásné předměty v přírodě kolem nás jsou i matematicky krásné. Čím dál více si to uvědomují nejenom matematikové, biologové  a další přírodovědci, ale také umělci. Jeden z nich  - španělský designér a 3D ilustrátor Cristóbal Vila to velmi názorně předvádí  ve svém videu.

Pokud si už umíte zavázat tkaničky, můžete další inspiraci ohledně jejich šněrování najít na stránce, která se  precizně zabývá šněrovacími metodami. Tady jsem se rovněž dočetl, že existuje téměř 2 biliónů možností jak je zavázat a ty nejzajímavější možnosti jsou zde také velmi názorně ukázány. Pokud zvládnete některou netradiční techniku šněrování, pak si můžete ušetřit více než polovinu běžného času, který šněrování věnujete.

Velikost obsahu plochy pravidelných rovinných obrazců se nejjednodušeji a zároveň nejpřesněji určí výpočtem podle vzorců na základě zjištěných rozměrů. Pokud chceme zjistit obsah plochy nepravidelných obrazců, pak můžeme rozdělit obrazce na pravidelné útvary, jejichž plochu lze spočítat nebo odměřit na milimetrovém papíru. K snadnému určení obsahu rovinné plochy nepravidelných obrazců se používá zařízení zvané polární planimetr.  Jeho princip měření je zajímavý. Jeho vodícím hrotem se objede po obvodu obrazce a obsah plochy se určí  z údaje bubínku, upevněného na rameni planimetru. Jednoduchý návod na jeho konstrukci si zde popíšeme.

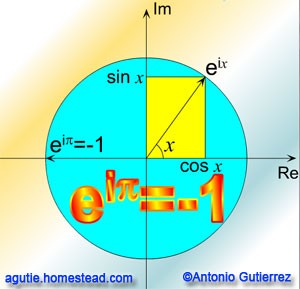Mezi nejkrásnější matematické rovnice patří Eulerova rovnost. Byla známa už počátkem 18. století, ale teprve Leonard Euler ji v roce 1748 "znovuobjevil" a hlavně ve svém díle zpopularizoval. Geometrický význam tohoto vztahu však tehdy nebyl znám. Euler tedy ve své práci uvedl rovnost:

e^ix = cosx + i.sinx,

která platí pro každé reálné číslo x. Velmi těsně spojuje goniometrické funkce, Eulerovo číslo e a druhou odmocninu z čísla –1 (imaginární jednotku i)

Když chceme spravedlivě a náhodně rozhodnout mezi dvěma možnými jevy, tak si obvykle házíme mincí. Stanovíme, jaký výsledek přísluší panně a jaký přísluší orlu. Mimochodem toto označení líce a rubu mince je u nás používáno ze staré korunové mince, kde byla na pohledové lícové straně vyobrazena klečící dívka, která sází lípovou ratolest. Pokud je mince v pořádku, pak pravděpodobnost, že padne panna nebo orel je stejná a sice ½. Co když ale máme podezření, že mince je falešná s tím, že pravděpodobnost jedné z možností je větší?

Zatímco v desítkové soustavě používáme k zápisu čísla až 10  možných číslic, ve dvojkové (binární) soustavě používáme k zápisu jen číslice dvě: 0 a 1. Tyto symboly je vhodné používat ve výpočetní technice, neboť odpovídají dvěma různým stavům elektrického obvodu (0 = vypnuto, 1 = zapnuto). Ve výrokové logice označujeme 0 jako nepravdivý výrok a 1 jako pravdivý výrok. Jak jsou tedy ve dvojkové soustavě tvořena čísla?

Hlavolam zvaný Rubikova kostka nepřestává od roku 1974, kdy byla vynalezena maďarským sochařem a architektem Ernő Rubikem, stále fascinovat matematiky. Při sledování soutěžících skládajících běžnou variantu hlavolamu 3x3x3 (speedcubing) bývá rekordmany  dosahováno časů pod 10 sekund. Další variantou je soutěžení ve složení kostky v co nejméně tazích. Američtí matematikové přišli nyní s tím, že všechny kombinace Rubikovy kostky se dají vyřešit do 20 tahů.