Velmi pěknou aplikací prvočísel v praxi jsou kódy knížek. Jsou označovány jako ISBN kódy a stejně jako rodná čísla jsou chráněny proti možné chybě samoopravným mechanismem. Tento systém mezinárodního standardního číslování knih - ISBN (International Standard Book Numbering) vznikl v Anglii na návrh profesora Gordona Fostera. Sdružení britských vydavatelů jej pověřilo návrhem jednoznačného číslování vydávaných knih. Foster v roce 1966 navrhl systém používající devíticiferné kódy. Ten byl zpočátku používán v Anglii a Postupně se rozšířil do více než 180 zemí. V České republice je zaveden od roku 1989. V tomto roce poprvé u nás vyšla také má nejoblíbenější kniha pod kódem ISBN 80-204-0023-0.

Pro přesná měření délek předmětů především ve strojírenství se používá posuvné měřítko - takzvaná šupléra (z německého Schub-lehre). Na ní si můžeme ukázat zajímavé praktické použití nesoudělných čísel. Měřítko se skládá ze dvou částí. Na pevné části je základní stupnice v níž je každý centimetr rozdělen na 10 mm. K pevné části pevně přiléhá posuvná část zvaná nonius, rozdělený na 10 stejně velkých dílků, které však dohromady měří jen 9 mm.

V praxi se osvědčují jednoduchá kritéria dělitelnosti přirozených čísel. Pokud jde například finanční hotovost rozdělit pro všechny zúčastněné stejným dílem, je to vždycky pozitivní. Jestliže znaky dělitelnosti jednocifernými čísly jsou notoricky známé, pak dělitelnost zejména některými prvočísly tak známá není. Uvádím zde znaky dělitelnosti od čísla 2 do čísla 19: 

Odkud ale tato pověra pochází? To nikdo přesně neví. Může se však datovat až do biblických dob (13. host na Ježíšově poslední večeři – Jidáš, který jej zradil). Ve středověku považovali pátek i číslo třináct za zlé znamení. Víra, že čísla ovlivňují naše životy - numerologie - však má dlouhou historii. Její stopy můžete sledovat až k následovníkům Pythagora, který se snažil popsat svět složený z čísel. Matematici a filozofové, kteří studovali pod vedením Pythagora, kombinovali čísla různým způsobem a snažili se jejich pomocí vysvětlit všechny jevy kolem sebe. Dnes se numerologie podle vědců stala para-vědou, něco jako bezvýznamné předpovědi astrologů. Matematici se shodují, že člověk vždy dokáže věci vyjádřit pomocí čísel, které si zvolí, záleží jen od míry snažení.   

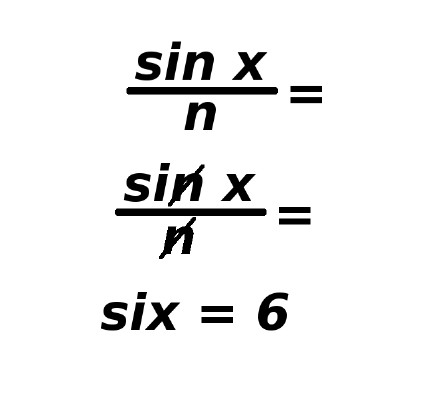Ve fyzice se setkáváme s nejrůznějšími zjednodušeními. Příkladem jednoho z matematických přibližných vztahů je sinx = x (přibližně). U tohoto vztahu se uvádí, že platí jen pro malé úhly. Když se ptáte pro jaké, dostane se vám odpovědi, že je to pro úhly menší než je 5°. Proč tomu tak je?

Nikomachos z Gerasy (1. – 2. st. n. l.) patří mezi novopythagorejce. Jeho dílo "Úvod do matematiky" je nejvýznamnější písemnou památkou pythagorejské školy. Je to na svou dobu vzniku velmi populárně psaná kniha. Vědecky pojat je pouze úvod do pythagorejské teorie čísel. Úrovní matematického pojetí však zůstává daleko za Eukleidem. Svoje tvrzení nedokazuje, pouze je podpírá konkrétními příklady. Některá jeho zjištění jsou matematicky krásná.

Letos uplynulo právě 35 let od vzniku nejznámějšího mechanického hlavolamu světa – Rubikovy kostky. Vynalezl jej v roce 1974 maďarský sochař a architekt Ernő Rubik. Kostky se začaly prodávat v miliónových sériích , nejrůznějších grafických a tvarových úpravách a staly se naprostým hitem u nás zejména v 80. letech. Nejběžnější typ se 3 vrstvami je složen z 26 dílů - 8 rohů (3 barvy), 12 hran (2 barvy) a 6 středů (jednobarevné). Celá konstrukce je spojena otáčivým mechanismem, který umožňuje libovolnou vrstvu pootočit o násobky 90°, pouze středy stran jsou nepohyblivé. Pokud je tato kostka náhodně promíchána, pak je úkolem řešitele poskládat kostku zpět do složeného tvaru. Pro kostku 3x3x3 je celkový počet kombinací 43 252 003 274 489 856 000. Jak se k tomuto úctyhodnému číslu přijde zjistíte detailně na

V matematice se snažíme používat jednoduché a názorné pomůcky pro vizuální představu množin, vztahů mezi nimi a operacemi s nimi. Vhodným nástrojem při zavádění a procvičování průniku, sjednocení, rozdílu množin a doplňku množiny v množině jsou Vennovy diagramy. Správné používání Vennových diagramů vyžaduje dobrou orientaci v těchto diagramech a pochopení vztahů mezi jednotlivými částmi konkrétního diagramu. Pomocí Vennových diagramů také můžeme řešit nejrůznější logické úlohy, které nám život přináší. Jejich další využití je při řešení slovních úloh, ve kterých se určují počty prvků konečných množin.

Matematikové patří ke stejnému živočišnému druhu jako my všichni. Zabývají se však čím dál více problémy, které však běžným smrtelníkům dávno nejsou zřetelné a to ani pokud se týká vlastního zadání. Tak jako by  připadala starověkým Řekům nepochopitelná a vzdálená myšlenka komplexních čísel nebo neeukleidovských geometrií, nám dnes připadá složitá moderní matematika. Ovšem to, co se řeší v matematice nyní, bude třeba časem považováno za běžnou matematiku 22. století.

Rodné číslo je identifikátorem osob v České republice, který přiřazuje každému obyvateli jedinečné číslo. Jde o 10-ti místné číslo (9-ti místné u lidí s datem narození do 1. 1. roku 1954). Je v něm nejenom ukrytý datum narození, pohlaví osoby, ale údajně i matrika a pořadové číslo narození. Kromě toho je v něm ukryta zajímavá kontrolní funkce. (Na zobrazené mapce ČR jsou oblasti rozdělené podle první číslice čísla následujícího za lomítkem.)