Vezmeme-li větší skupinu dat (například 1000) reprezentujících jakoukoliv přírodní veličinu (například soubor fyzikálních konstant nebo ceny zboží v místním supermarketu), jaká je pravděpodobnost, že určité číslo bude začínat jedničkou? Na první pohled je odpověď jasná: Počáteční číslovka může být 1, 2, 3,... až 9 (vyloučíme nulu, která může být libovolně přiřazena před jakékoliv číslo). Tedy pravděpodobnost výskytu jakékoliv číslovky na prvním místě je 1/9 = 0,111 neboli 11,1 %. Takže z 1000 čísel by 11,1 %, tj. zhruba 111 čísel, mělo začínat jedničkou (stejně jako dvojkou, trojkou atd.). Je to tak skutečně?

K vynalezení logaritmů došlo takřka současně a zcela nezávisle na několika různých místech. Logaritmy umožnily převést složitější početní výkon násobení (dělení, umocňování či odmocňování) na výkon jednodušší sčítání (odčítání, násobení, dělení) což se zvláště před rozšířením elektronických kalkulaček a počítačů využívalo při složitějších výpočtech prováděných ručně nebo mechanickými kalkulátory (které obvykle uměly jen sčítat). Pro usnadnění přepočtů existovaly logaritmické tabulky s předvypočítanými hodnotami logaritmů, případně logaritmické pravítko, mechanická pomůcka pro výpočty pomocí logaritmů.

Již před přibližně 2300 lety dokázal slavný matematik Eukleides, že existuje nekonečně mnoho prvočísel. Učinil tak ve dvacáté poučce v deváté knize svého slavného díla "Základy". Onen opravdu chytrý Řek došel ke svému důkazu následujícím postupem.

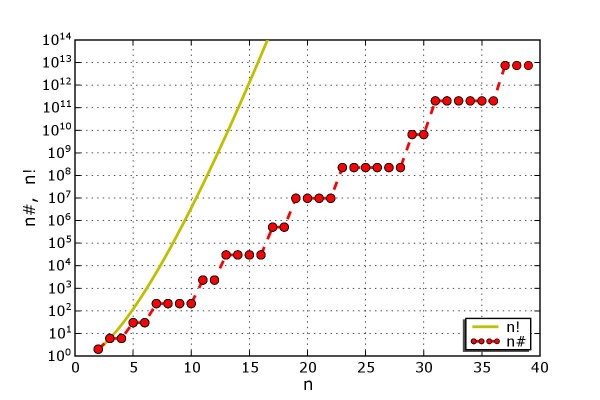
Kromě známějšího faktoriálu existuje méně známý primoriál. Abyste získali faktoriál, musíte vynásobit dané číslo všemi celými menšími čísly. Faktoriál čísla pět je tedy : 5! = 5 . 4 . 3 . 2 . 1 = 120. Primoriál získáme, když vynásobíme prvočíslo všemi menšími prvočísly.

Dnes se naučíme násobit po ruském způsobu na prstech. Toto násobení se používá pro součin čísel od 6 do 10. Nejprve podle obrázku přiřadíme každému z prstů obou rukou odpovídající číslo od 6 do 10. Pak násobená čísla - prsty rukou - spojíme podle dalšího obrázku.

Goldbachova hypotéza je jeden z nejstarších a nejslavnějších nevyřešených problémů matematiky, který patří do oblasti teorie čísel. Německý právník, pruský velvyslanec v Rusku a matematický samouk Christian Goldbach (1690 – 1764), který se v matematice zabýval především teorií čísel, zformuloval roku 1742 v dopise matematiku Eulerovi hypotézu, že každé přirozené číslo n větší než 5 je součtem nejvýše tří prvočísel.

Na solidní kalkulačce je spousta zajímavých funkcí. Všimli jste si někdy tlačítka s vykřičníkem? Není to varování před zmáčknutím tohoto tlačítka, ale označení funkce faktoriál. Faktoriál čísla n je součin všech přirozených čísel od jedné do daného čísla. Faktoriál zapisujeme pomocí čísla s vykřičníkem: n! Značení n! vyslovujeme jako "n faktoriál". Speciálně pro nulu byl vyčleněn faktoriál: 0! = 1. Například 5! je roven 5 × 4 × 3 × 2 × 1, tedy 120.

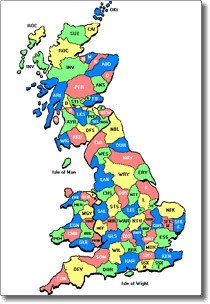
Tento problém pochází z matematické teorie grafů.  Prvním, kdo byl s tímto problémem spojován, je německý matematik a zakladatel topologie August Ferdinand Möbius. Na své přednášce z roku 1840 uvádí teoretické základy problému. O 12 let později se anglický student Frederic Guthrie pokoušel vybarvit mapu Anglie rozdělenou na hrabství. Chtěl ji vybarvit tak, aby každá oblast měla jinou barvu než oblast sousední. Jaký je nejmenší počet barev, který by na to stačil, pokud se sousední oblasti nikdy nestýkají pouze v bodě?

V roce 1979 vymyslel Howard Garns matematickou křížovku a publikoval ji v pod názvem "Number Place". Oblíbenou se stala v Japonsku, odkud se později vrátila zpět pod názvem Sudoku. Sudoku se stalo velmi populárním na konci roku 2004 ve Velké Británii a postupně se rozšiřuje

Vyrobte si děrovaný čtvercový koberec podle návodu. Jednotkový čtverec rozdělíme na 9 shodných čtverců a odstraníme vnitřek prostředního čtverce. Každý ze zbývajících čtverců rozdělíme znovu na 9 shodných čtverečků a znovu odstraníme v každém z nich jeho střední čtvereček. Po třetím kroku takové operace dostaneme útvar na obrázku. Když tuto operaci budeme dělat donekonečna, dostaneme útvar, který se nazývá Sierpińského koberec (Waclaw Sierpiński 1882 - 1969). Čemu se pak rovná obsah tohoto koberce?