Tento důkaz Pythagorovy věty nevymyslel kocour Garfield, jak si možná myslíte, ale 20. americký prezident James Garfield. Zběhl z akademické dráhy učitele matematiky k právům a stal se politikem. Dotáhl to až na amerického prezidenta, ale po 4 měsících v tomto úřadě byl na něj spáchán 2. července 1881 atentát. Kulky atentátníka jej sice přímo nezabily, ale jeho následky přivodily Garfieldovy dlouhodobě léčené zdravotní komplikace, kterým 19. září 1881 nakonec podlehl. Garfieldův důkaz Pythagorovy věty patří mezi ty méně obvyklé.
V nerovnostranném trojúhelníku můžeme sestrojit přímku, která prochází 3 významnými body v tomto útvaru. Prvním z bodů může být těžiště trojúhelníku, které získáme jako průsečík všech 3 těžnic trojúhelníku. Těžnice trojúhelníku spojují vrchol trojúhelníku ses tředem protější strany. Dalším z bodů je průsečík tří os stran trojúhelníku, který je zároveň středem kružnice trojúhelníku opsané. Třetím bodem je ortocentrum – průsečík všech výšek trojúhelníku.
Vzorec pro obsah kruhu lze odvodit nejrůznějšími způsoby. Jedno ze zajímavých odvození je s využitím vzorce pro obvod kruhu a ze vzorce pro obsah trojúhelníku. A když se k tomu dodá zajímavá grafická podoba pomocí řady korálků, pak je důkaz pěkně názorný.
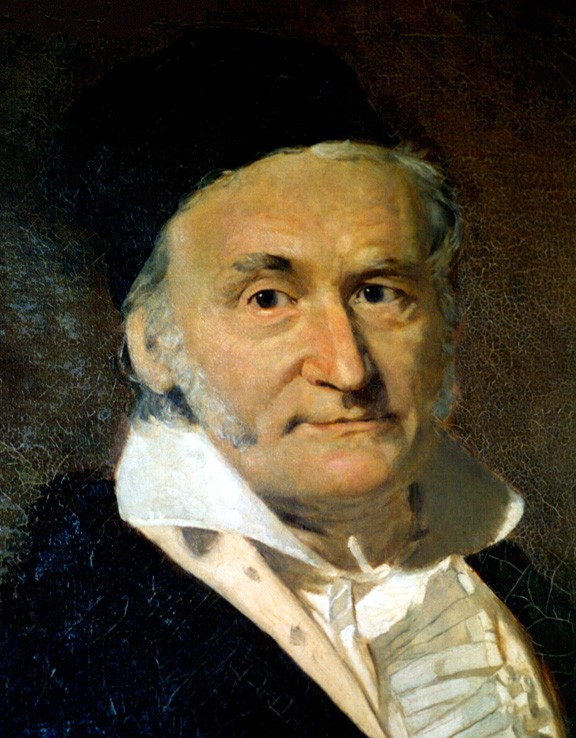Velikonoce patří k pohyblivým svátkům a jejich termín se odvozuje od první neděle po prvním jarním úplňku. Když však bude vycházet první jarní úplněk na neděli, budou se Velikonoce slavit až následující neděli. Velikonoční pondělí tak může nastat mezi 23. březnem až 26. dubnem. Kdy budou Velikonoce příští rok? Pokud nemáte k dispozici kalendář, pak si jejich termín můžete vypočítat podle postupu, který vymyslel významný německý matematik, astronom a fyzik Karl Friedrich Gauss (1777 - 1855).
Každým rokem 14. března zaznamenávám na těchto stránkách rekordní přístupy. Prvním rokem jsem si lámal hlavu, proč najednou v tento den návštěvnost webu Fyzmatik prudce vzrůstá, aby den následující klesla na standardní denní průměr. Po analýze nejzobrazovanějších článků za poslední měsíc mi bylo vše jasné. Zájem každoročně vzbuzuje článek o Ludolfově čísle p, který si v tento den vygooglují stovky lidí z celého světa. Mé stránky jsou ovšem v češtině a tak těmto návštěvníkům dnes nabízím známý Mathematical Pi Song. Dnes už vím, že 14. března se na celém matematickém světě slaví den čísla p. A čím si to tento den zasloužil? Který významný matematik zabývající se tímto číslem se v tento den narodil nebo zemřel? Vysvětlení je zcela jiné a prosté...
Při řešení rovnic se nevyhnete používání matematického znaku =. Každý ví, že je to rovnítko, matematický symbol, označující rovnost dvou objektů. Používaný symbol dvou stejně dlouhých úseček pochází od waleského matematika Roberta Recorda (1510 – 1558). Ten je použil ve svém spise The Whetstone of Witte (volně přeloženo "Brousek znalostí") z roku 1557 v rovnici uvedené na obrázku.
Římské číslice se i dnes používají na cifernících hodin, při označování kapitol v některých hodin, u označení pořadí panovníků nebo při označování letopočtů. K zápisu čísel stačí 7 římských číslic, které se zapisují pomocí vybraných písmen z abecedy. Tyto číslice vznikly z vyjadřování čísel pomocí rukou. Římská číslice I vznikla z vyjadřování čísel pomocí jednotlivých prstů, číslice V je tvar mezi roztaženým palcem a malíčkem jedné ruky, znamenající dlaň s pěti prsty. Číslice X znamenající 10 je spojením dvou dlaní rukou. K zapamatování římských číslic je možné používat několik mnemotechnických pomůcek.
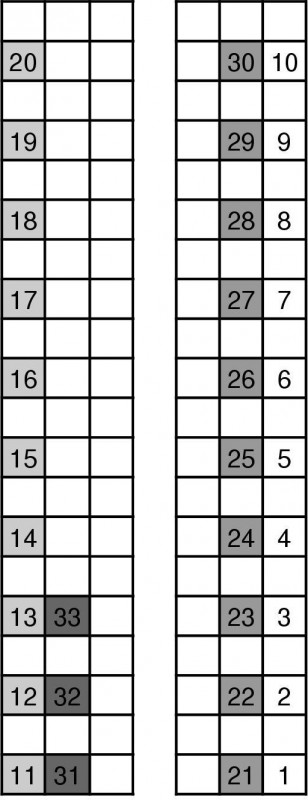Často po dlouhém odbavování a všech kontrolách na letišti nás ještě čeká dlouhé usazování cestujících v letadle. Pominu, že mnohé charterové linky a některé letecké společnosti nemají v usazování cestujících žádný systém a v uličce letadla pak vládne dokonalý chaos. Mnozí cestující blokují celé minuty uličku, dohadují se, kde vlastně sedí, pak se fotografují, či hrabou ve svých zavazadlech než je uloží do boxů atd. Americký astrofyzik Jason Steffen před několika lety přišel na způsob, jak při obsazování letadla ušetřit lidem nervy a čas. Podle jeho pokynů by v budoucnu mohly letecké společnosti podle palubních místenek optimalizovat rychlost nástupu, což nyní potvrdil experiment provedený v televizním pořadu This vs That.
Jednoduchá internetová hra na odhad a procvičení výpočtů se zlomky nás přivádí mezi nosnice Henriette a Güdhen. Zatímco se chystají snášet vejce, objeví se nám pod jejich bidýlky na číselné ose hnízdo, kterým můžeme pohybovat myší podle odhadovaného výsledku příkladu. Pokud odhadnete správný výsledek nebo jej dokonce správně vypočítáte, dopadne vejce do hnízda a podle rychlosti a správnosti vašeho výsledku získáváte body. Když je výsledek nesprávný, vejce se za pěkného zvukového efektu rozbije.
V technické praxi se setkáváme s potřebou zobrazování prostorových útvarů. I když dnes existují počítačové programy, které to pohodlně umožňují, je nutné se seznámit s pravidly zobrazování. Věda, která se zabývá zobrazováním prostorových útvarů do roviny (průmětny) se nazývá deskriptivní geometrie. Její počátky souvisejí se znázorňováním staveb na nákresy a plány. Už před 4300 lety používali Chaldejci pravoúhlé promítání na jednu průmětnu při stavbách silnic, akvaduktů, chrámů apod. i pyramid. zobrazovací metody byly zdokonalovány nejenom pro potřeby stavitelství, ale také pro potřeby malířství. Od 15. století se začala používat lineární perspektiva a po ní dochází k rozvoji rovnoběžného promítání, a to nejdříve kosoúhlého. To bylo využíváno především ve vojenství, a to hlavně k zobrazování celých měst nebo jejich významných částí.
