Collatzův problém 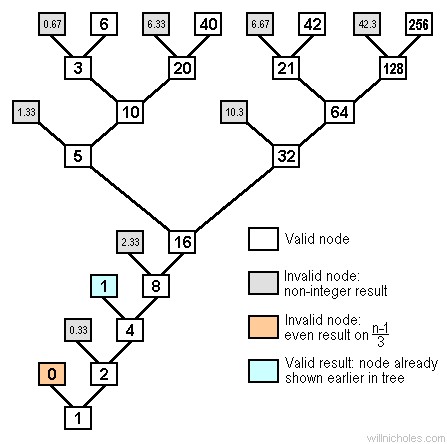je jedním z dosud nevyřešených matematických problémů. Je pojmenován po Lotharu Collatzovi, který jej poprvé formuloval v roce 1937. Tento problém je znám pod různými názvy: jako 3n + 1 problém, Ulamův problém (po Stanislawu Ulamovi), Syrakuský problém či sekvence ledové kroupy.

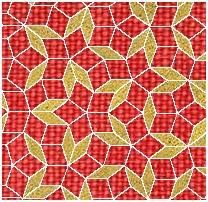Matematik si všímá problémů prakticky všude  – i na dlažbě. Zajímavé úlohy v počítačové grafice, geometrii, umění i architektuře hrají obrazce (dlaždice – z anglického termínu tiles), ze kterých je možné sestavovat mozaiky beze zbytku vyplňující nějakou předem známou plochu nebo i celou rovinu. S dělením roviny souvisí  právě dlažby. Pokrýt podlahu dlaždicemi stejného tvaru lze různě. Pokud chceme vydláždit rovinu dlaždicemi určitého typu, zjistíme, že takovými dlaždicemi mohou být pravidelné trojúhelníky, čtverce, obdélníky, kosočtverce, šestiúhelníky - ve všech těchto případech stačí dlaždice jediného typu k pokrytí roviny beze zbytku. K pokrytí roviny ovšem nevystačíme např. s pravidelnými pětiúhelníky, k nim musíme přibrat ještě další "doplňkovou" dlaždici – kosočtverec.

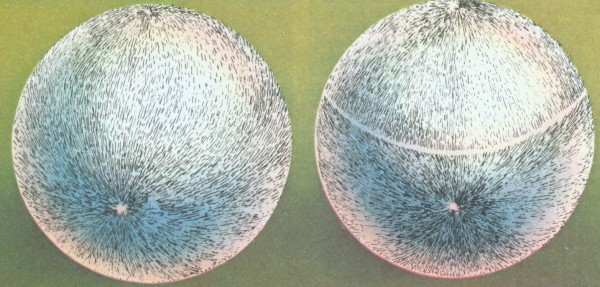Je topologickou pravdou, že jakkoli dlouhá zakroucená hadice má dva konce. Topologie převádí takové vžité představy do přesného matematického jazyka. Zabývá se těmi vlastnostmi objektů, které nezávisejí na změnách jejich tvaru, i kdyby byly sebevětší. Pro topologie je například každé jednoduché těleso bez děr koule, neboť kdyby bylo z měkkého těsta, dalo by se přeměnit na kouli, aniž bychom je trhali. Například neporušený ubrus je tedy koule, ale děravý ubrus už koulí není.

Zákon velkých čísel patří k nejčastěji špatně chápaným výsledkům počtu pravděpodobnosti a statistiky. Historie tohoto zákona začíná u Girolama Cardana (1501 – 1576). Ten tvrdil, že pravděpodobnost některého z možných jevů spojených s výsledky náhodného pokusu je rovna poměru mezi počtem možných výsledků,  ve kterých onen jev nastává, k počtu všech možných výsledků onoho pokusu. Například pravděpodobnost, že při hodu klasickou kostkou padne liché číslo je rovna poměru mezi počtem lichých výsledků (jsou 3) a počtem všech možných výsledků (je jich 6) – tedy  3/6 = ½.

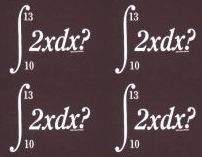Integrál je spolu s derivací nejdůležitější pojem matematické analýzy. Pojem integrálu je zevšeobecněním pojmů jako plocha, objem, součet či suma. Integrování je opačnou operací k derivování. Znak integrálu upoutá svým štíhlým tvarem, ale víte jak vůbec vznikl?

Vezmeme-li větší skupinu dat (například 1000) reprezentujících jakoukoliv přírodní veličinu (například soubor fyzikálních konstant nebo ceny zboží v místním supermarketu), jaká je pravděpodobnost, že určité číslo bude začínat jedničkou? Na první pohled je odpověď jasná: Počáteční číslovka může být 1, 2, 3,... až 9 (vyloučíme nulu, která může být libovolně přiřazena před jakékoliv číslo). Tedy pravděpodobnost výskytu jakékoliv číslovky na prvním místě je 1/9 = 0,111 neboli 11,1 %. Takže z 1000 čísel by 11,1 %, tj. zhruba 111 čísel, mělo začínat jedničkou (stejně jako dvojkou, trojkou atd.). Je to tak skutečně?

K vynalezení logaritmů došlo takřka současně a zcela nezávisle na několika různých místech. Logaritmy umožnily převést složitější početní výkon násobení (dělení, umocňování či odmocňování) na výkon jednodušší sčítání (odčítání, násobení, dělení) což se zvláště před rozšířením elektronických kalkulaček a počítačů využívalo při složitějších výpočtech prováděných ručně nebo mechanickými kalkulátory (které obvykle uměly jen sčítat). Pro usnadnění přepočtů existovaly logaritmické tabulky s předvypočítanými hodnotami logaritmů, případně logaritmické pravítko, mechanická pomůcka pro výpočty pomocí logaritmů.

Již před přibližně 2300 lety dokázal slavný matematik Eukleides, že existuje nekonečně mnoho prvočísel. Učinil tak ve dvacáté poučce v deváté knize svého slavného díla "Základy". Onen opravdu chytrý Řek došel ke svému důkazu následujícím postupem.

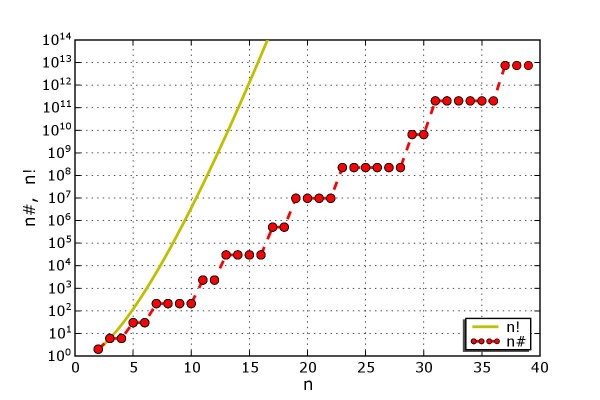
Kromě známějšího faktoriálu existuje méně známý primoriál. Abyste získali faktoriál, musíte vynásobit dané číslo všemi celými menšími čísly. Faktoriál čísla pět je tedy : 5! = 5 . 4 . 3 . 2 . 1 = 120. Primoriál získáme, když vynásobíme prvočíslo všemi menšími prvočísly.

Dnes se naučíme násobit po ruském způsobu na prstech. Toto násobení se používá pro součin čísel od 6 do 10. Nejprve podle obrázku přiřadíme každému z prstů obou rukou odpovídající číslo od 6 do 10. Pak násobená čísla - prsty rukou - spojíme podle dalšího obrázku.