Matematikové patří ke stejnému živočišnému druhu jako my všichni. Zabývají se však čím dál více problémy, které však běžným smrtelníkům dávno nejsou zřetelné a to ani pokud se týká vlastního zadání. Tak jako by  připadala starověkým Řekům nepochopitelná a vzdálená myšlenka komplexních čísel nebo neeukleidovských geometrií, nám dnes připadá složitá moderní matematika. Ovšem to, co se řeší v matematice nyní, bude třeba časem považováno za běžnou matematiku 22. století.

Rodné číslo je identifikátorem osob v České republice, který přiřazuje každému obyvateli jedinečné číslo. Jde o 10-ti místné číslo (9-ti místné u lidí s datem narození do 1. 1. roku 1954). Je v něm nejenom ukrytý datum narození, pohlaví osoby, ale údajně i matrika a pořadové číslo narození. Kromě toho je v něm ukryta zajímavá kontrolní funkce. (Na zobrazené mapce ČR jsou oblasti rozdělené podle první číslice čísla následujícího za lomítkem.) 

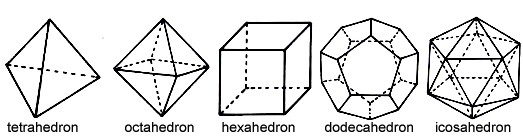Pravidelný mnohostěn je těleso, jehož stěny jsou tvořeny pravidelnými mnohoúhelníky (rovnostranný trojúhelník, čtverec, ...), jichž se v každém vrcholu stýká stejný počet. Pravidelné mnohostěny nazýváme platónská tělesa. Existuje jich právě 5, ačkoliv by se zdálo, že jejich počet může být libovolný. Platónská tělesa znali již ve starověku. Nazývají se podle řeckého filosofa Platóna  (5. – 4. stol př. n. l.), který učinil nauku o pravidelných mnohostěnech součástí svého idealistického názoru. V antickém období se hledáním pravidelných mnohostěnů zabývalo spousta matematiků. Mnohostěny byly občas přiřazovány jednotlivým "živlům", předpokládalo se, že právě takový tvar mají atomy. Podle samotného Platóna se oheň skládal ze čtyřstěnů, vzduch z osmistěnů,, voda z dvacetistěnů a země z krychlí. Obrys světa pak tvořil dvanáctistěn.

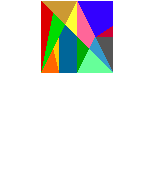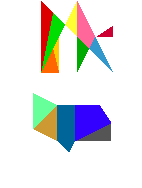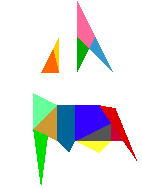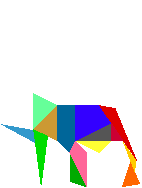Stomachion je pravoúhelník, jehož strany jsou v poměru 1:2,. Je rozřezán na 14 dílů. V překladu z řečtiny označuje stomachion "to, co vyvolává zlost". Jde o hru, kdy z uvedených dílů se skládají různé obrazce podobně jako ve známějším tangramu. Části pracoúhelníku lze k sobě přikládat libovolnými stranami, přitom podle Archiméda není nutné přikládat části těsně. Při zobrazení každé figury (kohout, slon, větrný mlýn, slepice...) se však má upotřebit všech 14 dílů.

Blíží se konec školního roku a objevuje se sem tam suplovaná hodina matematiky. Všechno učivo z uplynulého ročníku je probráno a zbývá čas na procvičování matematického myšlení. Osvědčenými matematickými hrami jsou sudoku a Matematico. Zatímco k sudoku je potřeba mít namnožené mřížky s předvyplněnými čísly, ke hře matematiko potřebujeme čistý papír tužku a připravené karty s čísly.

Určitě znáte některý z matematických problémů, ve kterém figuruje koza. Připomenu: vlk, koza a zelí se mají přepravit na druhou stranu řeky.... Jenže tohle zvíře vystupovalo v matematickém problému, který byl prezentován na počátku 90. let 20. století v USA v populární show Montyho Halla "Let's Make a Deal". V programu tohoto konferenciéra se mohli diváci zúčastnit soutěže o automobil. Úkol, který měli splnit, byl vcelku jednoduchý. Ve studiu se nacházely troje zavřené dveře. Za jedněmi z nich se skrývalo auto a za dalšími dvěma živé kozy.

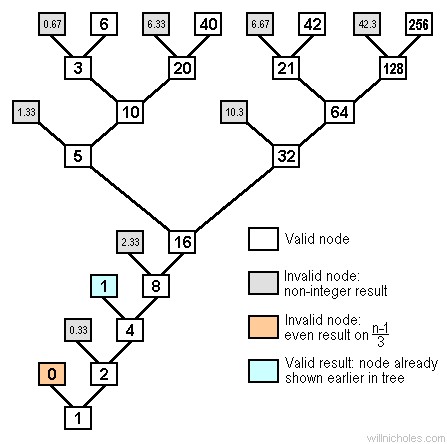Collatzův problém je jedním z dosud nevyřešených matematických problémů. Je pojmenován po Lotharu Collatzovi, který jej poprvé formuloval v roce 1937. Tento problém je znám pod různými názvy: jako 3n + 1 problém, Ulamův problém (po Stanislawu Ulamovi), Syrakuský problém či sekvence ledové kroupy.

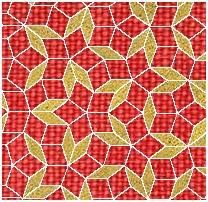Matematik si všímá problémů prakticky všude  – i na dlažbě. Zajímavé úlohy v počítačové grafice, geometrii, umění i architektuře hrají obrazce (dlaždice – z anglického termínu tiles), ze kterých je možné sestavovat mozaiky beze zbytku vyplňující nějakou předem známou plochu nebo i celou rovinu. S dělením roviny souvisí  právě dlažby. Pokrýt podlahu dlaždicemi stejného tvaru lze různě. Pokud chceme vydláždit rovinu dlaždicemi určitého typu, zjistíme, že takovými dlaždicemi mohou být pravidelné trojúhelníky, čtverce, obdélníky, kosočtverce, šestiúhelníky - ve všech těchto případech stačí dlaždice jediného typu k pokrytí roviny beze zbytku. K pokrytí roviny ovšem nevystačíme např. s pravidelnými pětiúhelníky, k nim musíme přibrat ještě další "doplňkovou" dlaždici – kosočtverec.

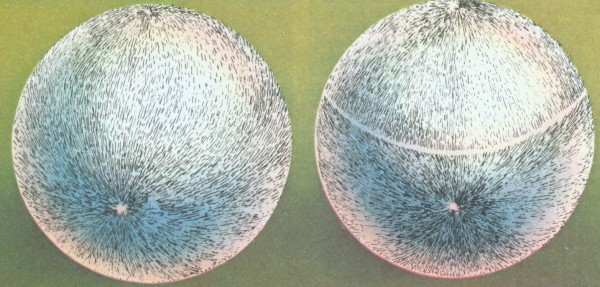Je topologickou pravdou, že jakkoli dlouhá zakroucená hadice má dva konce. Topologie převádí takové vžité představy do přesného matematického jazyka. Zabývá se těmi vlastnostmi objektů, které nezávisejí na změnách jejich tvaru, i kdyby byly sebevětší. Pro topologie je například každé jednoduché těleso bez děr koule, neboť kdyby bylo z měkkého těsta, dalo by se přeměnit na kouli, aniž bychom je trhali. Například neporušený ubrus je tedy koule, ale děravý ubrus už koulí není.

Zákon velkých čísel patří k nejčastěji špatně chápaným výsledkům počtu pravděpodobnosti a statistiky. Historie tohoto zákona začíná u Girolama Cardana (1501 – 1576). Ten tvrdil, že pravděpodobnost některého z možných jevů spojených s výsledky náhodného pokusu je rovna poměru mezi počtem možných výsledků,  ve kterých onen jev nastává, k počtu všech možných výsledků onoho pokusu. Například pravděpodobnost, že při hodu klasickou kostkou padne liché číslo je rovna poměru mezi počtem lichých výsledků (jsou 3) a počtem všech možných výsledků (je jich 6) – tedy  3/6 = ½.