Hledání prvočísel má velký význam při moderních metodách šifrování a kódování. Zatímco je velmi snadné vynásobit jednotlivá čísla a získat tak jejich součin, tak daleko složitějším problémem je mnohdy rozložit (dekódovat) velké číslo na součin prvočísel. Proto se také matematikové snaží nacházet nová a nová prvočísla. Na jejich hledání se specializuje projekt GIMPS (Great Internet Mersenne Prime Search), díky němuž vygeneroval computer matematika Curtise Coopera z University of Missouri dosud největší známé prvočíslo, obsahující 22 338 618 číslic za sebou. To má o pět milionů číslic více než u předcházejícího prvočísla nalezeného v roce 2013.

Čárový kód znáte především z výrobků, které si kupujete. Ve skladech slouží k levné a velmi přesné orientaci ve zboží pomocí rychlého sběru dat. V obchodě jej načte prodavač čtečkou a po počítačovém zpracování je výrobek váš. U nás se nejběžněji používá čárový kód typu EAN 13 (nebo redukovaný 8). Čárový kód se skládá z černotiskem vytištěných tmavých pruhů a ze světlých mezer s přesně stanovenou šířkou. Běžné laserové snímače čárového kódu vyzařují červené světlo, které je tmavými čarami pohlcováno a naopak světlými mezerami odráženo. Snímač ve čtečce zjišťuje rozdíly v odrazivosti a ty transformuje v elektrické signály odpovídající šířce čar a mezer. Pak jsou signály převedeny v číslice, popř. písmena, jaká obsahuje příslušný čárový kód a porovnávány s tabulkou přípustných kombinací. Pokud je posloupnost v tabulce nalezena, je prohlášena za odpovídající znakový řetězec. Zajímavostí je, že při snímání čárového kódu není nutné, aby čtečka jela kolmo k jednotlivým čarám, protože poměr mezi tloušťkami čar a mezer zůstává stejný. Jak je možné, že při použití čárových kódů se počet chyb snižuje až na jednu milióntinu?

Flexagony jsou v geometrii ploché modely sestavené skládáním proužků papíru, které mohou být různě přehnuté a překlopené. Flex označuje v angličtině ohýbat. Tím vznikají nejenom zajímavé struktury, ale často je využíváno toho, že na papíru jsou na obou stranách zobrazené různé objekty, které se otáčením zobrazují do různých souvislostí. Flexagony jsou obvykle čtvercové nebo obdélníkové (tetraflexagony ) nebo hexagonální ( hexaflexagony ). Předpona přidaná k názvu flexagonu udává uvést počet ploch, které model může zobrazovat, včetně dvou stran (přední a zadní), které jsou viditelné před ohnutím. 

Tento důkaz Pythagorovy věty nevymyslel kocour Garfield, jak si možná myslíte, ale 20. americký prezident James Garfield. Zběhl z akademické dráhy učitele matematiky k právům a stal se politikem. Dotáhl to až na amerického prezidenta, ale po 4 měsících v tomto úřadě byl na něj spáchán 2. července 1881 atentát. Kulky atentátníka jej sice přímo nezabily, ale jeho následky přivodily Garfieldovy dlouhodobě léčené zdravotní komplikace, kterým  19. září 1881 nakonec podlehl.  Garfieldův důkaz Pythagorovy věty patří mezi ty méně obvyklé.

V nerovnostranném trojúhelníku  můžeme sestrojit přímku, která prochází 3 významnými body v tomto útvaru. Prvním z bodů může být těžiště trojúhelníku, které získáme jako průsečík všech 3 těžnic trojúhelníku. Těžnice trojúhelníku spojují vrchol trojúhelníku ses tředem protější strany.  Dalším z bodů je průsečík tří os stran trojúhelníku, který je zároveň středem kružnice trojúhelníku opsané. Třetím bodem je ortocentrum – průsečík všech výšek trojúhelníku.

Vzorec pro obsah kruhu lze odvodit nejrůznějšími způsoby. Jedno ze zajímavých odvození je s využitím vzorce pro obvod kruhu a ze vzorce pro obsah trojúhelníku. A když se k tomu dodá zajímavá grafická podoba pomocí řady korálků, pak je důkaz pěkně názorný.

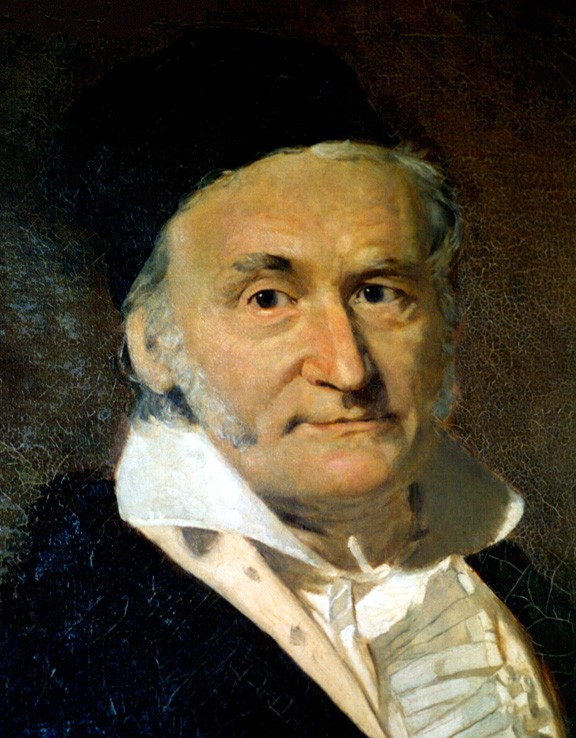Velikonoce patří k pohyblivým svátkům a jejich termín se odvozuje od první neděle po prvním jarním úplňku. Když však bude vycházet první jarní úplněk na neděli, budou se Velikonoce slavit až následující neděli.  Velikonoční pondělí tak může nastat mezi 23. březnem až 26. dubnem.  Kdy budou Velikonoce příští rok? Pokud nemáte k dispozici kalendář, pak si jejich termín můžete vypočítat podle postupu, který vymyslel významný německý matematik, astronom a fyzik Karl Friedrich Gauss (1777 - 1855).

Každým rokem 14. března zaznamenávám na těchto stránkách rekordní  přístupy. Prvním rokem jsem si lámal hlavu, proč najednou v tento den návštěvnost webu Fyzmatik prudce  vzrůstá, aby den následující klesla na standardní denní průměr.  Po analýze nejzobrazovanějších článků za poslední měsíc mi bylo vše jasné. Zájem každoročně vzbuzuje článek o Ludolfově čísle p, který si v tento den vygooglují stovky lidí z celého světa. Mé stránky jsou ovšem v češtině a tak těmto návštěvníkům dnes nabízím známý Mathematical Pi Song. Dnes už vím, že 14. března se na celém matematickém světě slaví den čísla p. A čím si to tento den zasloužil? Který významný matematik zabývající se tímto číslem se v tento den narodil nebo zemřel? Vysvětlení je zcela jiné a prosté...

Při řešení rovnic se nevyhnete používání matematického znaku =.  Každý ví, že je to rovnítko, matematický symbol, označující rovnost dvou objektů. Používaný symbol dvou stejně dlouhých úseček pochází od  waleského matematika Roberta Recorda (1510 – 1558). Ten je použil ve svém spise The Whetstone of Witte (volně přeloženo "Brousek znalostí") z roku 1557 v rovnici uvedené na obrázku.

Římské číslice se i dnes používají na cifernících hodin, při označování kapitol v některých hodin, u označení pořadí panovníků nebo při označování letopočtů. K zápisu čísel stačí 7 římských číslic, které se zapisují pomocí vybraných písmen z abecedy. Tyto číslice vznikly z vyjadřování čísel pomocí rukou. Římská číslice I vznikla z vyjadřování čísel pomocí jednotlivých prstů, číslice V je tvar mezi roztaženým palcem a malíčkem jedné ruky, znamenající dlaň s pěti prsty. Číslice X znamenající 10 je spojením dvou dlaní rukou.  K zapamatování římských číslic je možné používat několik mnemotechnických pomůcek.