Dnes se naučíme násobit po ruském způsobu na prstech. Toto násobení se používá pro součin čísel od 6 do 10. Nejprve podle obrázku přiřadíme každému z prstů obou rukou odpovídající číslo od 6 do 10. Pak násobená čísla - prsty rukou - spojíme podle dalšího obrázku.

Goldbachova hypotéza je jeden z nejstarších a nejslavnějších nevyřešených problémů matematiky, který patří do oblasti teorie čísel. Německý právník, pruský velvyslanec v Rusku a matematický samouk Christian Goldbach (1690 – 1764), který se v matematice zabýval především teorií čísel, zformuloval roku 1742 v dopise matematiku Eulerovi hypotézu, že každé přirozené číslo n větší než 5 je součtem nejvýše tří prvočísel.

Na solidní kalkulačce je spousta zajímavých funkcí. Všimli jste si někdy tlačítka s vykřičníkem? Není to varování před zmáčknutím tohoto tlačítka, ale označení funkce faktoriál. Faktoriál čísla n je součin všech přirozených čísel od jedné do daného čísla. Faktoriál zapisujeme pomocí čísla s vykřičníkem: n! Značení n! vyslovujeme jako "n faktoriál". Speciálně pro nulu byl vyčleněn faktoriál: 0! = 1. Například 5! je roven 5 × 4 × 3 × 2 × 1, tedy 120.

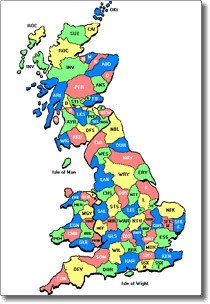
Tento problém pochází z matematické teorie grafů.  Prvním, kdo byl s tímto problémem spojován, je německý matematik a zakladatel topologie August Ferdinand Möbius. Na své přednášce z roku 1840 uvádí teoretické základy problému. O 12 let později se anglický student Frederic Guthrie pokoušel vybarvit mapu Anglie rozdělenou na hrabství. Chtěl ji vybarvit tak, aby každá oblast měla jinou barvu než oblast sousední. Jaký je nejmenší počet barev, který by na to stačil, pokud se sousední oblasti nikdy nestýkají pouze v bodě?

V roce 1979 vymyslel Howard Garns matematickou křížovku a publikoval ji v pod názvem "Number Place". Oblíbenou se stala v Japonsku, odkud se později vrátila zpět pod názvem Sudoku. Sudoku se stalo velmi populárním na konci roku 2004 ve Velké Británii a postupně se rozšiřuje

Vyrobte si děrovaný čtvercový koberec podle návodu. Jednotkový čtverec rozdělíme na 9 shodných čtverců a odstraníme vnitřek prostředního čtverce. Každý ze zbývajících čtverců rozdělíme znovu na 9 shodných čtverečků a znovu odstraníme v každém z nich jeho střední čtvereček. Po třetím kroku takové operace dostaneme útvar na obrázku. Když tuto operaci budeme dělat donekonečna, dostaneme útvar, který se nazývá Sierpińského koberec (Waclaw Sierpiński 1882 - 1969). Čemu se pak rovná obsah tohoto koberce?

Friedrich Gauss bývá označován za největšího matematika od dob Archimédových, ne-li za největšího matematika vůbec. Narodil se roku 1777 v Brunšviku jako syn zedníka a vodního mistra, který se také staral o vodotrysky a jiné věci s vodou spojené. V prvních letech se Gauss učil dříve počítat než mluvit, pak teprve začal své známé a příbuzné "prosit o písmena", a najednou uměl číst , aniž kdo pořádně věděl, kde k tomu přišel.V sedmi letech začal chodit do obecné školy, kde měl ve třídě 100 spolužáků, ale nijak mezi nimi nevynikal. Teprve v devíti letech na sebe upozornil příhodou, která se dodnes traduje.

Jak převádět dlouhá čísla do libozvučné písmenné kombinace, která by umožnila jejich snazší zapamatování? Je to mnohem úspornější řešení než říkanky, ve kterých jsou cifry zakódovány pomocí počtu písmen ve slovech. Uvedl jsem tu před časem říkanky k Ludolfovu číslu p a každý si asi pamatuje "šetři se osle” jako 6 378 k určení poloměru Země.